Pileup
Last updated October 7, 1998
Table of pileup fractions for
all tests
Memo in
Postscript format: HEXS Flat Field Pileup Analysis, Stephen Jones, 8/2/97.
Memo in Postscript format: An
Analytical ACIS Pileup Model, Brian McNamara, 10/2/97.
Memo in Postscript format: ACIS Pileup:
Analysis of XRCF Phase H Data, Joel Kastner, Kester Allen, & Kenny
Glotfelty, 2/24/98.
1. MONOCHROMATIC PILEUP VS. A SIMPLE PILEUP MODEL
Figure 1 shows the correlation between the photon pileup
fraction and the number of detected photons per CCD frame.
The data were extracted from 15 on-axis, focussed, point spread function
and count rate linearity measurements obtained
at the XRCF during Phase H testing. The x axis shows the number of incident
X-ray photons per ACIS frame, calculated as
fBND × EA (HRMA + ACIS) × tf ;
fBND is the mean X-ray flux (photons/sec/cm2) at
the HRMA entrance aperture, EA (HRMA + ACIS) is the current baseline model
for the product of the HRMA effective area × ACIS QE × optical
blocking filter transmission, and tf is the ACIS frame
time. The y axis shows the degree of pileup determined using two
methods. The diamonds represent the
ratio of the sum of photons in the n = 2-3 or n = 2-4 spectral pileup peaks
to the total number of photons in the main peak (n=1) + the pileup peaks,
calculated as
pp= sumn > 1 [An × n] /
sumn >= 1 [An × n],
where An is the area under the main peak or pileup peak.
Figure 1.

This plot is also available in Postscript
format.
The degree of photon pileup was determined for all grades (diamonds)
and for ASCA grades 02346 (connected triangles). The data, which range
in energy between 1.486 keV and 6.4 keV, were obtained with both the
front-illuminated and back-illuminated CCDs.
In addition, we calculated the degree of event pileup as
pe = sumn > 1 [An] / sumn >=1 [An].
These data are plotted as squares in Fig. 1, and are tabulated in
Table 1. The degree of event pileup is roughly a factor of two
smaller than the degree of photon pileup.
The data are compared in Fig. 1 to an analytic ACIS pileup
model (see the memo entitled
``An Analytical ACIS Pileup Model''
1997, by B.R. McNamara).
The solid and dashed lines were produced using the McNamara (1997)
pileup model. The model has one free parameter: the encircled energy
(detected photons) within the central pixel island detection cell in the limit
of zero pileup, approximately 2.1 pixels.
In order to scale the model to the data, we measured the encircled
energy fraction within 2.1 pixels for the
three tests with the lowest degree of pileup in our study (H-IAS-PI-1.041,
H-IAI-CR-1.001,
H-IAS-CR-1.002).
The photon pileup fractions for these tests are less than 8%.
It is necessary to scale the model using the encircled energy radius
in the limit of zero pileup because, the measured encircled energy radius
migrates outward as the degree of pileup increases (see below).
The mean encircled energy within the central detection cell (2.1 pix)
for these tests was found to be epsilon(r)=61%. The scaled model (dashed line) fits the
all grade (diamonds; appropriate for the model comparison) photon pileup
fraction quite well over the full range of the data.
The degree of photon pileup is underestimated when using G02346 data because
of grade migration.
The model systematically overestimates the degree of event pileup,
unless epsilon(r) <<61%, which is inconsistent with the data.
This simple pileup model is able to predict reasonably well the degree
of pileup in XRCF data spanning a broad range of energy and pileup
conditions, for both front and back illuminated CCDs. The solid line
shows the degree of pileup expected for an on-axis point source on
orbit (minus gravity, finite distance, and finite source size). The
degree of pileup for a given number of counts per frame will be ~2×
larger on orbit because of the sharper PSF.
2. PILEUP SIGNATURES IN FOCUSSED IMAGES
In order to correct for pileup in flight science data, the observer
will need some understanding of the source flux (degree
of pileup) and the shape of the unpiled spectrum.
These are in general unknown quantities. We therefore need some
independent way of estimating the degree of pileup that does
not require that the spectrum and flux be known.
We have found at least three characteristics of the focussed point
spread function that are sensitive to the degree of pileup:
the encircled energy radius, the slope of the point spread function
in the core as a function of event grade, and the integrated area
of the core of the point spread function (PSF) as a function of event
grade.
The change in the 50%, 70%, and 90% encircled energy radius as a
function of the detected number of photons per frame for
the tests shown in Fig. 1 is shown in Fig. 2. Fig. 2 shows the increase in the encircled
energy radius with increasing flux. This trend is due to decrease in
the number of detected events in the core of the PSF relative to the
wings of the PSF caused by pileup in the core. The trend is most
obvious and has the least scatter when plotting the 50% encircled
energy radius, which is most sensitive to the number of detected
events in the core of the PSF.
Figure 2.
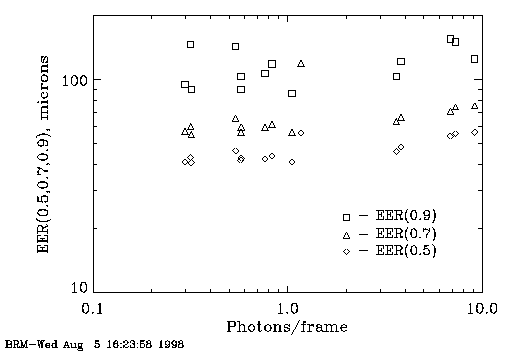
This plot is also available in Postscript
format.
We now ask how sensitive is the encircled energy radius to the
degree of pileup for purposes of estimating the degree of
pileup without knowledge of the incident flux. In Fig. 3 we plot the photon pileup fraction against the
50% encircled energy radius (EER(0.5)) on the left axis, and we
compare this to the photon pileup fraction plotted against the number
of photons per CCD frame on the right axis (i.e. Fig. 1). The solid curve is the pileup model fit to
the photon pileup fraction as a function of the number of photons per
frame (Fig. 1), and the dashed curve is a second
order polynomial fit to the EER(0.5) vs the photon pileup
fraction. This plot shows that the EER(0.5) is relatively insensitive
to the degree of pileup for pileup fractions less than 40%, or about 2
photons per frame. The sensitivity of EER(0.5) increases sharply as
the degree of pileup increases above 40%.
Figure 3.

This plot is also available in Postscript
format.
Most science observations should be planned so that the degree
of pileup is considerably less than 40%, and we expect most
to be in the few to 10% range. We therefore investigated
more sensitive measures of pileup. In Fig. 4 we
plot the change in the integrated area of the PSF profile A(G) between
G02346 and all grades, extracted from 2 pixel-wide slices
(Y-direction) for each focussed image. Inspection of these data for
each test show that the area under the G02346 PSF decreases with
respect to the PSF for all grades as pileup increases (See Table X
and associated data). This is the result of grade migration.
Similarly in Fig. 5 we plot the change in the peak
amplitude of the PSF between all grades and G02346. We plot the pileup
model and
data (right axis) in Figs. 4 & 5 as we did in Fig. 3. The dashed curve in Fig. 4
is a third order polynomial fit to A(G) vs pileup fraction (squares),
and the dashed curves in Fig. 5 are two linear fits
to P(G) vs pileup fraction. The first is fit to the range
Pp=0.05-0.4 and the second fits the range
Pp=0.4-1.0.
Figure 4.
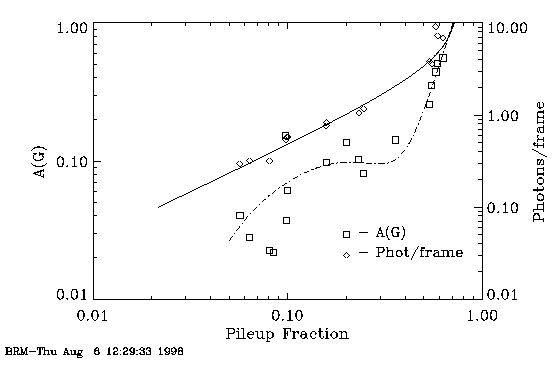
This plot is also available in Postscript
format.
We note the following from these figures:
both P(G) and A(G) are more sensitive to the degree of pileup
for Pp=0.05-0.4 than is EE(0.5). However the trend with
Pp is weak in this range and there is considerable scatter.
In general, P(G)~A(G)~0.5 × Pp.
the slopes in the trends between P(G) and A(G) vs Pp increase
sharply at Pp=0.4, where P(G)~A(G)~Pp
Figure 5.

This plot is also available in Postscript
format.
3. CONCLUSIONS
1) The in-focus, on-axis, monochromatic PSF images show a well
defined trend between pileup fraction (photon and event) and
the number of photons per CCD frame determined using BND
measurements and the AXAF-ACIS effective area model.
2) The one parameter, analytic pileup model proposed by McNamara
predicts the photon pileup fraction as a function of the
number of detected photons per frame to within several percent.
However, the model systematically overpredicts the event
pileup fraction as a function of the number of detected photons
per frame by ~2×.
3) We have shown that the structure of the PSF as a function
of photon event grade can be used to estimate the degree
of pileup for nearly monochromatic, focussed, on-axis data.
However, the sensitivity of the PSF structure to pileup
is weak for pileup fractions below ~40%. A spectrum-independent
means of estimating the degree of pileup in science observations
will be important when attempting to model and remove pileup
from the observed spectra. The sensitivity of the PSF structure to
pileup may increase for modest pileup levels with the sharper,
on-orbit PSF.
— B.R. McNamara, A. Ware
Comments to cxccal@cfa.harvard.edu




