Postscript version of this document
Alexey Vikhlinin
March 2, 2000; updated August 2000; updated December 2000
The quantum efficiency of the ACIS FI CCDs decreases at high energies and far from the read-out as a result of the CTI. This memo describes the measurement of this effect using multiple pointings to G21.5-0.9 at the CCD temperature -110C.
G21.5-0.9 was observed in a series of pointing in node 0 of I1, node 2 of I3, and node 2 of S2. Observations were made in July 2000; ACIS temperature was temporarily increased to -110 C. The table lists the observation details and the CTI coefficients (from Brian McNamara).
obsid chip node chipY CTI/1e-6
1772 i1 0 124 135.6
1773 i1 0 304 135.6
1774 i1 0 484 135.6
1775 i1 0 694 135.6
1776 i1 0 904 135.6
1777 i3 2 304 179.4
1778 i3 2 484 179.4
1779 i3 2 694 179.4
1780 s2 2 304 216.2
1781 s2 2 484 216.2
1782 s2 2 904 216.2
I extract the source spectra in PI channels in the same regions in
sky coordinates. ARFs are calculated using the HRMA effective area file
hrmaD1999-07-22axeffaN0004.fits, vignetting file
hrmaD1999-07-22vignetN0003.fits, and the spatially uniform CCD
QE from acisD1997-04-17qeN0002.fits. The QE curves are
individually calibrated for each CCD and presumably are accurate at the
readout.
Responce matrices have been generated using the version
_D1999-09-16fef_piN0002.fits of FEFs for -110C.
For perfectly calibrated CCD QE, HRMA vignetting, and RMFs, these spectra should produce identical fits in XSPEC. If any deviation of the data from the model are observed, this is interpreted as the change of QE or possibly, mirror vignetting.
Since we want to compare the observed spectra of G21.5-0.9 and the Coma
cluster in different chip positions, we first need to correct for the
CTI-caused gain variations across the CCDs. I used
acis_process_events with the acisD1999-09-16gainN0004.fits
gain table to recompute photon energies and PI channels.
The reference spectrum was derived in the 1-9 keV band from S3 pointings (on-axis observations), with CCD QE corrected using QEU files from Norbert Schulz and Sara-anne Taylor.
I tried both power law and broken power law models.
Simple power law fit (Fig. 1) gives the best fit parameters:
---------------------------------------------------------------------------
mo = wabs[1]( powerlaw[2] )
Model Fit Model Component Parameter Unit Value
par par comp
1 1 1 wabs nH 10^22 2.310
2 2 2 powerlaw PhoIndex 1.844
3 3 2 powerlaw norm 1.9903E-02
---------------------------------------------------------------------------
There seems to be an excess over the power law model at E>7keV. This may
be due to spatial variations of the power law index (Pat Slane's paper): we
have a mixture of steep and flat spectra, and an attempt to fit it with a
single power law produces ``hard excess''. To model this excess, I also
tried the broken power law model (Fig. 2):
---------------------------------------------------------------------------
mo = wabs[1]( bknpower[2] )
Model Fit Model Component Parameter Unit Value
par par comp
1 1 1 wabs nH 10^22 2.301 +/- 0.2688E-01
2 2 2 bknpower PhoIndx1 1.844 +/- 0.1995E-01
3 3 2 bknpower BreakE keV 6.500 frozen
4 4 2 bknpower PhoIndx2 1.506 +/- 0.2069
5 5 2 bknpower norm 1.9849E-02 +/- 0.5635E-03
---------------------------------------------------------------------------
Below I used the broken power law model for the reference spectrum because
it seems to fit the data better and to be more physically motivated. All
conclusions are the same for the simple power law model.
Figures 3 and 4 show the ratio of the spectra obtained in FI chips and the S3 model. Here I will concentrate on the data above 2 keV.
The red points in Fig 3 correspond the I1 spectrum at
CHIPY=124. This region is near the readout and presumably, should not be
affected by the CTI. Indeed, the I1/S3 ratio at this CHIPY is consistent
with 1 within ![]() .
Note that the I1,CHIPY=124 pointing is 7'off-axis, while the S3 data is near the aim point. Therefore, good agreement
between the spectra shows that the vignetting calibration is good.
.
Note that the I1,CHIPY=124 pointing is 7'off-axis, while the S3 data is near the aim point. Therefore, good agreement
between the spectra shows that the vignetting calibration is good.
The CHIPY=904 spectrum in Fig 3 shows strong deviations
from the model at ![]() keV. Most likely, this is caused by the QE
drop due to CTI. Figure 4 gives more examples. All
these spectra show that although the amplitude of the effect varies as a
function of CHIPY and node,
keV. Most likely, this is caused by the QE
drop due to CTI. Figure 4 gives more examples. All
these spectra show that although the amplitude of the effect varies as a
function of CHIPY and node,
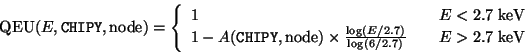 |
(1) |
![\includegraphics[height=0.9\linewidth,angle=-90]{i1y124-i1y904.ps}](img8.gif) |
![\includegraphics[height=0.49\linewidth,angle=-90]{i1y904-s2y904.ps}](img9.gif)
![\includegraphics[height=0.49\linewidth,angle=-90]{i1-i3-s2-y484.ps}](img10.gif) |
Figure 5 show the CHIPY dependence of the QE drop at 6 keV for July 2000 observations.
| (2) |
Values of parameters A0, Y0, and ![]() determine the correction as
a function of CHIPY in each node. Within the current accuracy of
calibration, A0 should be the same in all chips, while the values of
Y0 and
determine the correction as
a function of CHIPY in each node. Within the current accuracy of
calibration, A0 should be the same in all chips, while the values of
Y0 and ![]() take different values in ACIS-I and S2:
take different values in ACIS-I and S2:
| chip | A0 | Y0 | |
| I0,I1,I2,I3 | 0.155 | 540 | 350 |
| S2 | 0.155 | 350 | 200 |
![\includegraphics[height=0.6\linewidth]{plotcor-newonly.ps}](img13.gif) |
The spectra in Fig. 4 show that the data in all FI
chips at E<2 keV is ![]() % below the model fit to the S3 data. This
is even more prominent in I1 spectra at CHIPY=124 and 904
(Fig. 3). At E>2 keV, the spectrum at CHIPY=124 is in
excellent agreement with the S3 model; this is expected because no
degradation is expected at low CHIPY's. However, below 2 keV, this spectrum
is
% below the model fit to the S3 data. This
is even more prominent in I1 spectra at CHIPY=124 and 904
(Fig. 3). At E>2 keV, the spectrum at CHIPY=124 is in
excellent agreement with the S3 model; this is expected because no
degradation is expected at low CHIPY's. However, below 2 keV, this spectrum
is ![]() below the model.
below the model.
Coma cluster observation also shows this problem (Fig 6).
Figure 7 shows that the ratio of 1-1.8 keV fluxes in FI chips and S3 is the same in all nodes, and shows no obvious dependence on the off-axis angle or CHIPY.
The discrepancy at low energies may represent a problem with cross-calibration of the CCD QE between S3 and FI devices. It is also possible that RMF inaccuracies (either BI or FI or both) mimic the QE change at low energies. It is unclear at present which QE (BI or FI) is correct, but spectral fits to the galaxy cluster data suggest that it is the FI chips' QE that needs a correction by a factor of 0.93, if one uses the current (as of Jan 2001) RMFs.
![\includegraphics[height=0.6\linewidth,angle=-90]{coma_lowe.ps}](img16.gif) |
![\includegraphics[height=0.6\linewidth]{plotcor12.ps}](img17.gif) |