


|

|
This memorandum provides a brief summary of the non-linearities of the LETG+HRC-S dispersion relation and how we have mapped out these wavelength distortions across the HRC-S detector. It also gives a short description of the Perl script corrlam which applies a correction to reduce the non-linearities of the dispersion relation and illustrates the results of its applications. These corrections were incorporated into the degap solution hrcsD1999-07-22gaplookupN0002.fits as part of CALDB 3.2.0 in Nov 2005 and all subsequent updates.
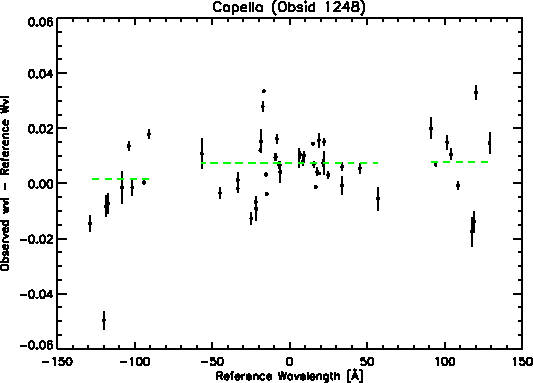
The LETG+HRC-S dispersion relation is known to approximately a few parts in 10000. For data processed with CIAO version 3.1 or later, the Root Mean Square (RMS) of the difference in observed versus theoretical wavelengths for detected, reasonably unblended lines with accurately known rest wavelengths, is 0.014Åacross the entire LETG+HRC-S wavelength range of -165 to +175Å.
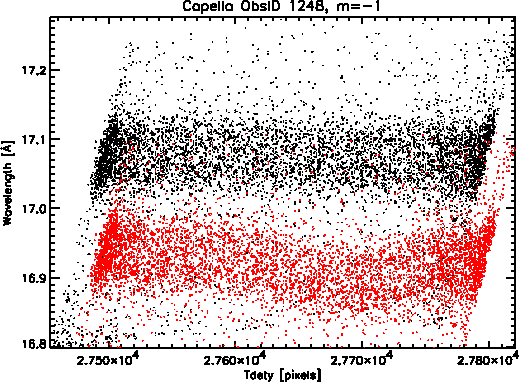
Uncertainties in the LETG+HRC-S wavelength positions are currently dominated by non-linearities in the dispersion relation, which can cause deviations of wavelength positions by as much as 0.05Å. These deviations are caused by the non-linear imaging distortions of the HRC-S detector, and are illustrated in Figure 1. The photons shown here are distributed along the detector dispersion axis (tdety) due to the nominal telescope dither. For observations made with normal model pointing, the telescope dithers in a lissajous pattern, spreading out the photons in both the dispersion and cross-dispersion directions, spanning a width of ~300 pixels or 40 arcseconds. In Figure 1, it is clear that the photons (shown in red) of the Capella Fe XVII emission line ``wobble'' non-linearly across tdety. These non-linearities are also apparent in the dispersion relation as seen in Figure 2.
In order to map out the non-linearities of the dispersion relation, we approach the data in wavelength versus tdety coordinate space as shown in Figure 1. As explained in the previous section, photons are spread across the detector by the telescope dither. Therefore, for any given emission line, we can split up the events into a number of bins along the detector dispersion axis (tdety). Then we histogram the events within each tdety bin, in wavelength, and measure the wavelength position by fitting a modified Lorentzian function to each histogram. By repeating this process for a number of lines located on different regions in tdety, we are able to map out the non-linearities of the dispersion relation along the detector. We subtract the theoretical wavelengths from the measured wavelengths (Δλ = λ - λ0) and fit a spline to Δλ as a function of tdety to obtain our final wavelength correction.
We have recently released a Perl script called corrlam written by Pete Ratzlaff. This script works on level 1.5 or level 2.0 event lists and computes new wavelength positions of photons by interpolating the Δλ as a function of tdety corrections. These wavelength corrections are read in as an ASCII file, with two columns for Δλ and tdety. The corrections are applied only to dispersed photons within a selected source region, specified by the cross-dispersion angle tg_d. By default, only events with absolute values of tg_d less than 1.33e-2 degrees are corrected, though the maximum allowed tg_d can be altered.
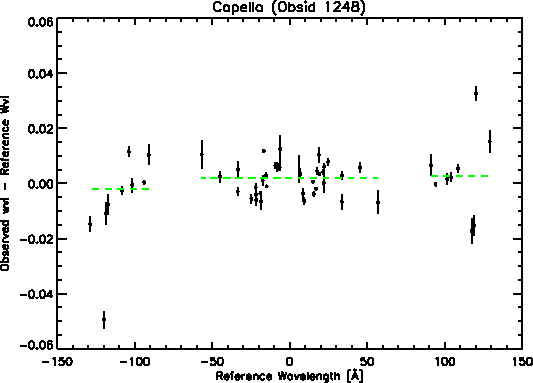
By applying these corrections, the non-linearities of the dispersion relation are greatly reduced. We are at present lacking the appropriate data to derive corrections for much of the outer plates. However, significant improvements in the non-linearities observed on the whole central plate are observed. Figure 3 shows the dispersion relation for Capella data with wavelength corrections applied. The RMS over the entire wavelength range has gone down from 0.014Å to 0.010Å. Across the central plate, the RMS has gone down by a factor of two, from 0.012Å to 0.006Å. Figure 1 also shows improvement for wavelength corrected data, which is shown in black.
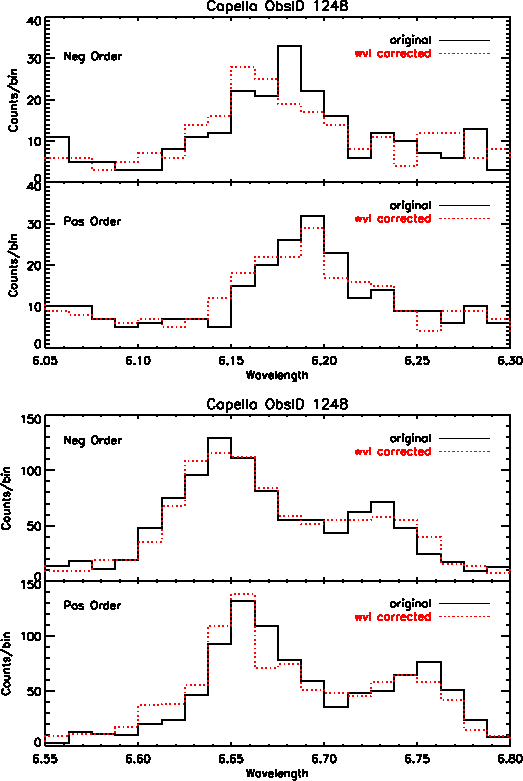
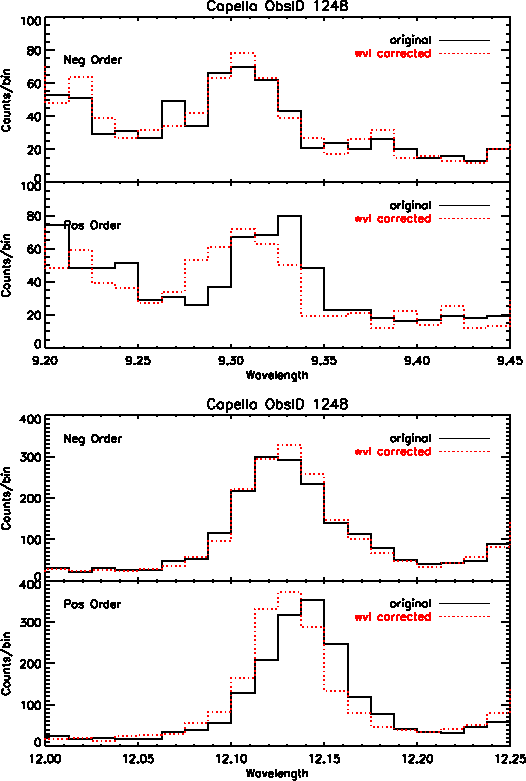
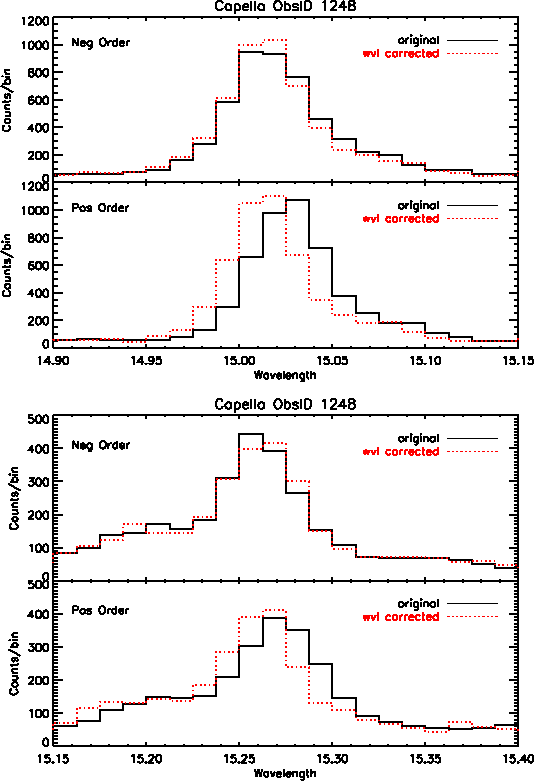
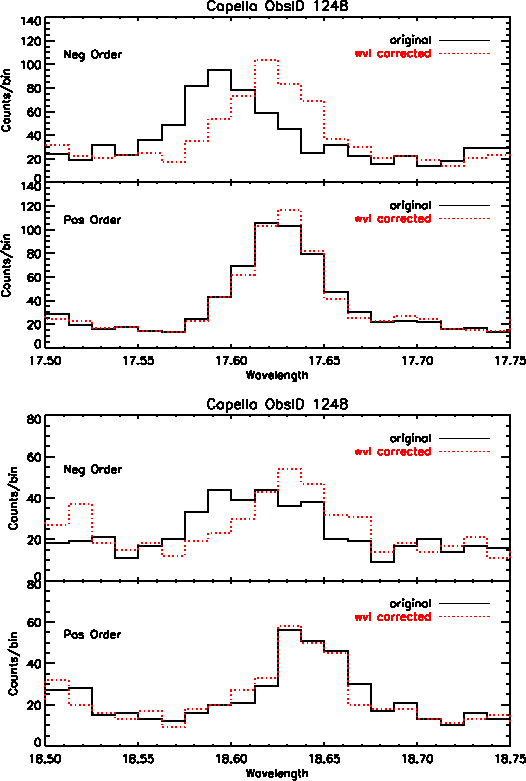
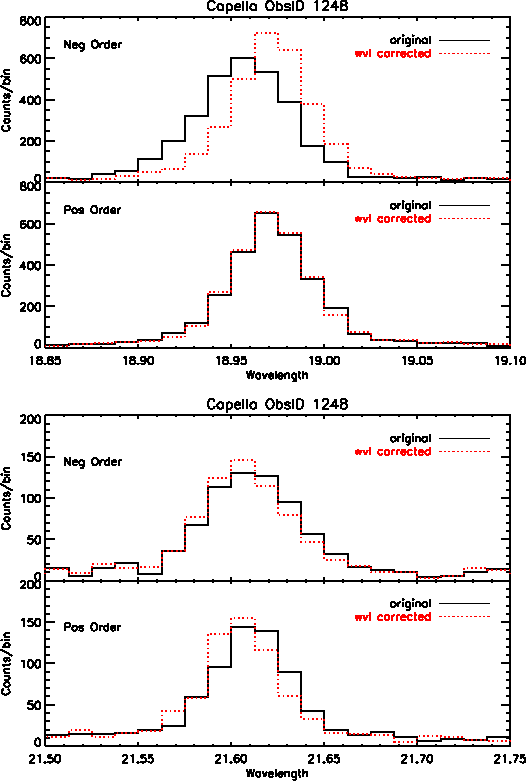
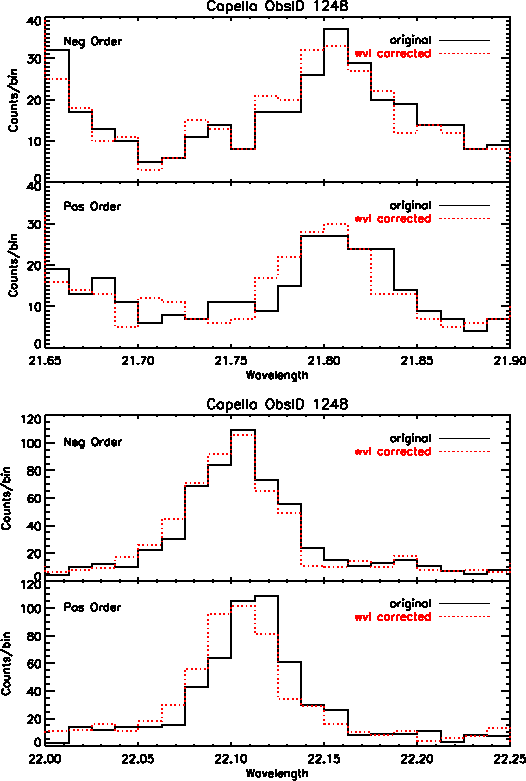
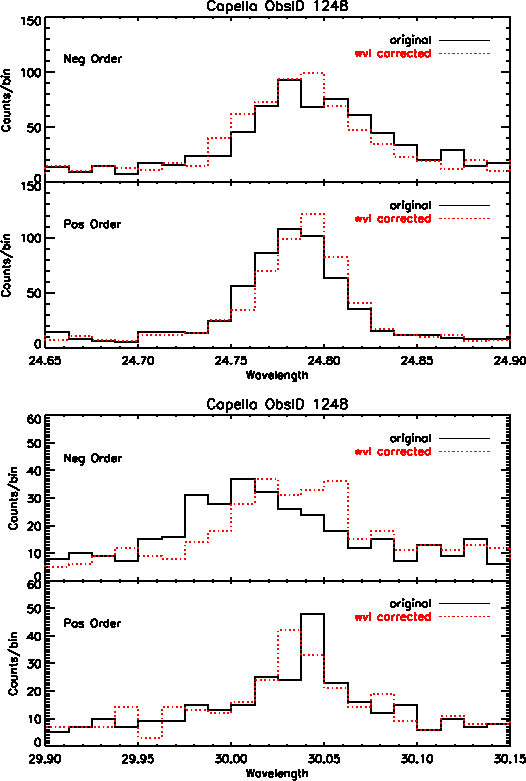
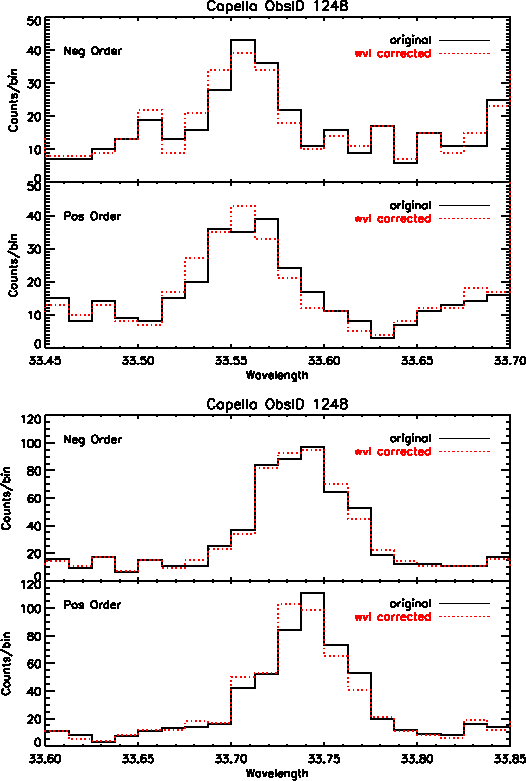
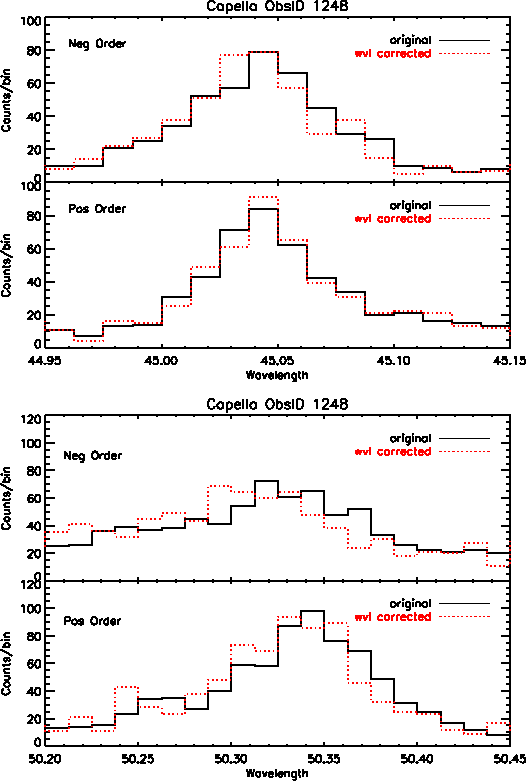
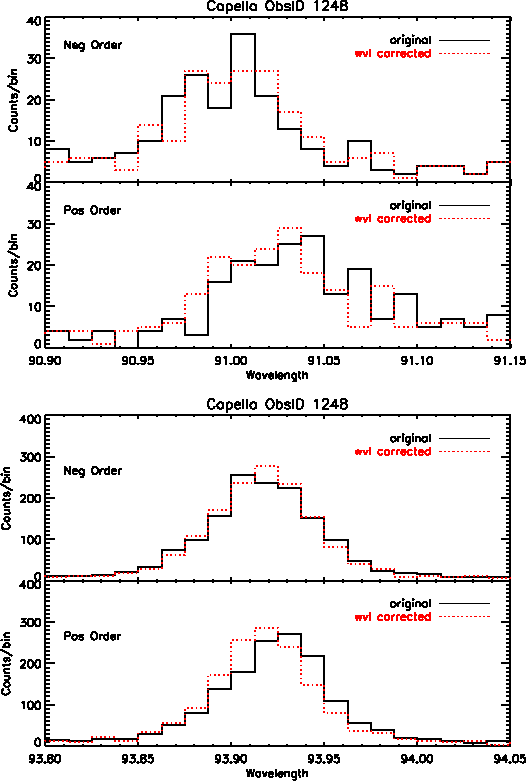
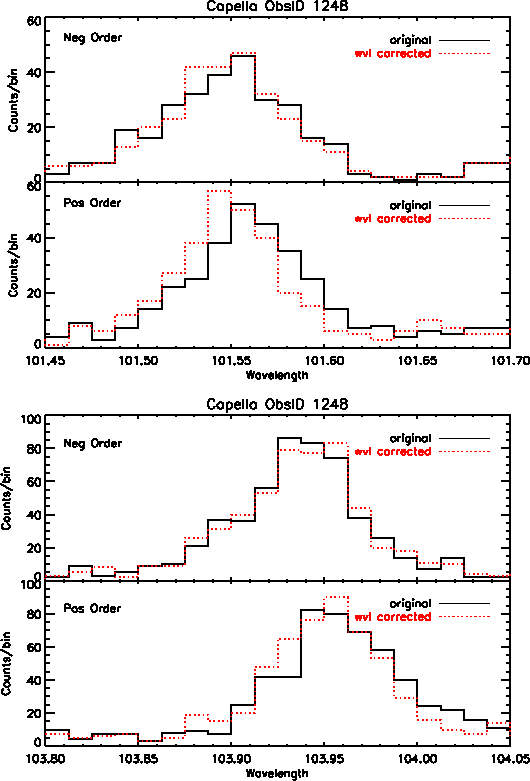
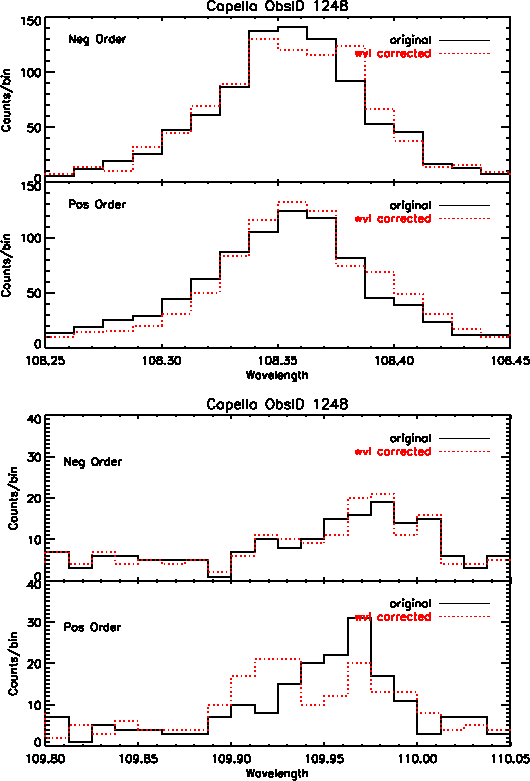
In addition to better accuracy in wavelength positions, we also see improvement in the line widths of many profiles, particularly on the central plate. However, many of the lines at longer wavelengths show little to no improvement because there are minimal wavelength corrections available at this time for data on the outer plates. Figure 4 shows Capella emission lines before and after the wavelength corrections were applied, for first order positive and negative events.
Please see the following for a more detailed discussion of the LETG+HRC-S dispersion relation non-linearities:
 |
 |
 |
 |


Last modified: 10/09/18
 |
The Chandra X-Ray
Center (CXC) is operated for NASA by the Smithsonian Astrophysical Observatory. 60 Garden Street, Cambridge, MA 02138 USA. Email: cxcweb@head.cfa.harvard.edu Smithsonian Institution, Copyright © 1998-2004. All rights reserved. |