

The following setion describes how the parts of the HRC hardware that perform event processing effect deadtime. Subsequent sections describe a computer simulation of the timing aspects of event processing and presents results from simulations for a range of input event rates which includes rates higher than the telemetry limit. Algorithms for determining the deadtime for rates both above and below the telemetry saturation limit are given. The final section compares the simulation results to measurements using ``flight-like'' electronics.
When the HRC MCPs are triggered by an event, it is counted and a series of hardware checks are performed to decide whether it should be processed and telemetered to the ground; this takes ~ 19.5 µs. If the event passes these checks it is counted as a valid event and the hardware processing that generates the telemetered event information is usually started. The processing will not occur if the hardware is already processing an event. From the time of the trigger to the time that the event information for telemetry has been generated is 68.5 µs. The HRC hardware is effectively ``dead'' to event processing during the 19.5 µs interval for the rejected events or the 68.5 µs interval for the accepted events. In simple terms these two times are the deadtime per rejected and accepted events respectively.
The HRC contains a hardware buffer that queues events for output into the telemetry slots. This ``primary'' science FIFO is large enough to hold the event information for 128 events. If events arrive faster than they can be telemetered, the FIFO will fill. Once it is full the hardware will hold the last event it receives, stop processing, and wait until one event has been removed from the FIFO; at this point it moves the event information it is holding into the FIFO and resumes processing. It is the fact that the hardware stops processing when the FIFO fills that creates the possibility for telemetry saturating deadtime. Even though the ``valid'' events are not being processed, they are still being counted.
In an effort to understand the HRC performance at sustained rates near telemetry saturation, we have written a set of software tools that simulates the process. The simulation operates in a series of steps.
The simulation starts with the generation of event times; a Poissonian process is simulated by generating a sequence of times with an exponential distribution of times between events. The mean event rate is controlled by the mean of the exponential distribution. These event times are piped to a tool that determines where the times occur relative to the telemetry major frames and minor frames. Additional information that can be used for other simulation purposes are also generated.
The event time information is then passed on to a tool that simulates how the HRC hardware processing works. All events are assumed to have passed the hardware tests, i.e. they are considered to be ``valid'' events. An event time is compared to the previous time to see if it arrived while the hardware was processing that event; if so it is counted as a piled-up event and not put into the FIFO storage space. If the event wasn't piled-up, the event time is compared to the current telemetry time to see if events should be taken from the FIFO.
If the time of the next telemetry slot occurs before the event time the event information is taken from the FIFO storage space and the major frame, minor frame, and event slot within the minor frame in which the event is telemetered is added to it. This process is repeated as many times as necessary, either the time of the slot is after the event time or there are no more events in the FIFO storage space.
If the time of the next telemetry slot is after the event time, the FIFO is checked to see if there is room for an event; if there is the event timing information is put into the FIFO storage space. If the FIFO is full, the event is not put into the FIFO storage space. The time from when the FIFO fills to when the next set of event information is transfered from the FIFO storage space to a telemetry slot is accumulated. At the end of the simulation the total time spent with the FIFO full is reported along with the total number of events input, the number of telemetered events, the number of piled-up events, and the number of events that occurred while the FIFO was full.
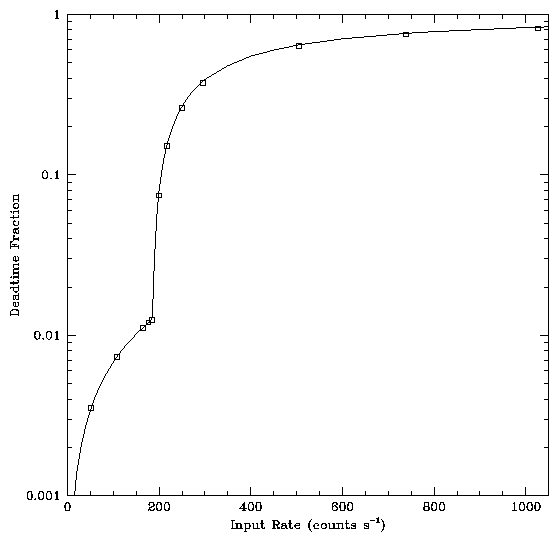
Simulator runs where performed for a range of mean event rates up to 1050 events s-1. Each simulation was run for an exposure of 1000 s. Table 1 contains the summary results from several simulation runs. As expected, the time spent with the FIFO full is zero until the mean rate is higher than the telemetry saturation rate. For rates above the telemetry saturation rate the deadtime increases rapidly with event rate. The deadtime fraction is plotted as a function of mean input rate in Figure 1.
| Number of Events | Time | ||||
| Mean Rate | Total Valid | Telemetered | Piled-up | FIFO-full | FIFO-Full |
| 10 | 10016 | 10007 | 9 | 0 | 0.000 |
| 100 | 100090 | 99422 | 668 | 0 | 0.000 |
| 150 | 150250 | 148721 | 1529 | 0 | 0.000 |
| 180 | 180233 | 177996 | 2237 | 0 | 0.000 |
| 185 | 185284 | 182857 | 2365 | 62 | 0.403 |
| 190 | 190312 | 184493 | 2501 | 3318 | 18.065 |
| 195 | 195317 | 184489 | 2636 | 8192 | 43.714 |
| 200 | 200346 | 184514 | 2788 | 13044 | 67.718 |
| 210 | 210412 | 184511 | 3090 | 22811 | 112.388 |
| 220 | 220362 | 184515 | 3385 | 32462 | 152.731 |
| 230 | 230257 | 184514 | 3694 | 42049 | 188.999 |
| 240 | 240361 | 184511 | 4030 | 51820 | 223.909 |
| 250 | 250327 | 184515 | 4354 | 61458 | 254.340 |
| 260 | 260596 | 184515 | 4679 | 71402 | 283.804 |
| 270 | 270627 | 184516 | 5062 | 81049 | 311.018 |
| 280 | 280634 | 184516 | 5413 | 90705 | 336.072 |
| 290 | 290517 | 184515 | 5795 | 100207 | 358.590 |
| 300 | 300579 | 184516 | 6195 | 109868 | 381.057 |
| 350 | 349832 | 184517 | 8333 | 156982 | 466.721997 |
| 400 | 399440 | 184516 | 10793 | 204131 | 535.607309 |
| 450 | 449640 | 184516 | 13551 | 251573 | 586.421435 |
| 505 | 504242 | 184517 | 16973 | 302752 | 632.676754 |
| 600 | 599854 | 184517 | 23961 | 391376 | 690.467608 |
| 740 | 739840 | 184517 | 36493 | 518830 | 748.298812 |
| 800 | 799881 | 184517 | 42688 | 572676 | 768.222602 |
| 1000 | 1000362 | 184517 | 66294 | 749551 | 815.157201 |
| 1050 | 1050192 | 184517 | 72955 | 792720 | 823.445800 |
In addition to the information from the events, the HRC telemeters the total event rate (total triggers of the MCP in 1 s intervals) and the valid event rate (those triggers that pass the hardware tests). We can use these to derive the instrument deadtime.
At rates below telemetry saturation, the deadtime td for a selected interval is given by:
| (1) |
At rates above telemetry saturation a simple approximation to the deadtime is given by
| (2) |
Table 2 gives the results of these data collections. The ``root name'' of each telemetry data set is given; these names give the date-time stamp of the start of the data collection. The average input event rate is determined from the total number of events counted by the scaler in the 100 s interval; the statistical uncertainty is given. The average total and valid event rates are the means of the values of the samples in the telemetry file for the given run; the uncertainty is the standard deviation of the samples. The average telemetered event rate is given by the total number of events in the telemetry file for the given run divided time duration of the telemetry. The time duration of the telemetry file is given by the number of minor frames that it contains times the duration of a minor frame (0.25625 s). The uncertainty on the telemetered event rate is solely statistical.
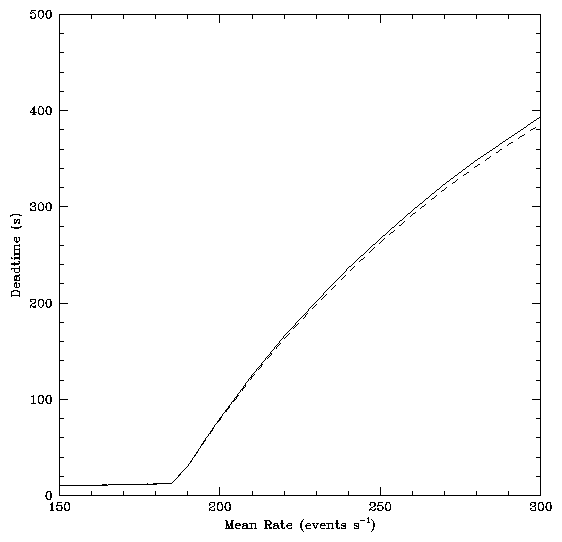
As expected, the telemetered event rate saturates at ~ 184.4 events s-1 as the input rate rises above this level. Figure 2 shows the deadtime fraction calculated from the data in table 2 using the algorithms given in section 4; the plotted curve is the deadtime fraction given by simulation runs. The deadtime corrected rates are in included in table 2. The deadtime corrected rates are in good agreement with the input rates below the telemetry saturation point (184.4 events s-1) and in reasonable agreement, systematically low by less than 2%, for input rates up to 5 times the telemetry saturating rate.
| Average Event Rates (counts s-1) | |||||
| Data Set | Input | Total | Valid | Telemetered | DT Corrected |
| 1999167.134447 | 51.57±0.72 | 51.34±3.98 | 51.34±3.98 | 51.40± 0.73 | 51.58 |
| 1999167.134819 | 107.72±1.04 | 107.56±4.74 | 107.56±4.74 | 107.17±1.05 | 108.00 |
| 1999167.135106 | 164.23±1.28 | 163.78±4.98 | 163.78±4.98 | 162.65±1.31 | 164.5 |
| 1999167.135417 | 177.08±1.33 | 176.28±4.69 | 176.28±4.69 | 175.31±1.34 | 177.4 |
| 1999167.135736 | 184.25±1.36 | 184.17±5.28 | 184.16±5.28 | 182.44±1.39 | 184.7 |
| 1999167.140029 | 200.09±1.41 | 199.15±4.61 | 199.15±4.61 | 184.38±1.38 | 199.2 |
| 1999167.140357 | 217.85±1.48 | 217.30±6.08 | 217.30±6.08 | 184.47±1.43 | 217.3 |
| 1999167.140648 | 250.02±1.58 | 249.48±5.46 | 249.48±5.46 | 184.42±1.38 | 249.5 |
| 1999167.140946 | 295.34±1.72 | 293.62±5.81 | 293.62±5.81 | 184.40±1.45 | 293.6 |
| 1999167.141241 | 505.38±2.25 | 501.89±6.09 | 501.88±6.07 | 184.38±1.41 | 501.9 |
| 1999167.141529 | 739.13±2.72 | 730.64±6.48 | 730.64±6.48 | 184.47±1.43 | 730.6 |
| 1999167.141824 | 1026.02±3.20 | 1008.76±7.68 | 1008.76±7.68 | 184.36±1.39 | 1009.00 |
Dr. Michael Juda
Harvard-Smithsonian Center for Astrophysics
60 Garden Street, Mail Stop 70
Cambridge, MA 02138, USA
Ph.: (617) 495-7062
Fax: (617) 495-7356
E-mail: mjuda@cfa.harvard.edu