Building the LSF library for Chandra CALDB
| Introduction |
| LSF Reference Data |
| >Building LSFPARMS |
| Caveats |
| Validation |
| Summary |
| Other Links |
| isis |
| mit/cxc |
| ciao |
| caldb |
Assumptions for building LSF
There are three major assumptions that we make to build the LSF library for Chandra CALDB:- MARX provides a perfect description of Chandra grating instruments,
- CIAO/DS tools perform tasks as designed,
- the HRMA system (e.g., focus) is stable in a long run.
Steps for Building LSF
The steps to build LSFs are as follows:- Run MARX simulations for mono-energetic beams,
- Generate a 2-D histogram of photon distribution per grating per order from MARX simulated dataset,
- Per a fixed extraction width, generate an integrated 1-D line profile from the 2-D histogram image,
- Perform multi-component fitting (2 Gaussian + 2 Lorentzian) to parameterize the 1-D profile,
- Evaluate encircled energy fraction,
- Repeat this process for various energy values and extraction widths,
- Record and tabulate the measured values; interpolate them with uniform grid points later,
- Bundle the interpolated values into a FITS file.
Examples of Line Profile fitting
Earlier on 1-D line profiles were fitted with one Gaussian and one Lorentzian functions for ACIS-S/HETG. However we note that these 2-component fit do not provide adequate description of the profile in general. Hence two Gaussian and two Lorentzian functions are now being utilized.Gaussian and Lorentzian functions are defined an in the following forms:
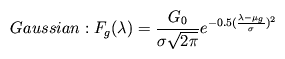
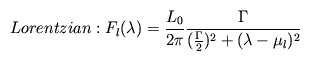
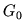 and
and 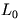 refers to Gaussian and Lorentzian amplitude terms,
refers to Gaussian and Lorentzian amplitude terms,
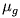 and
and 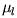 represent line centroid positions for Gaussian
and Lorentzian component respectively,
represent line centroid positions for Gaussian
and Lorentzian component respectively, 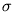 and
and 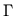 are
Gaussian and Lorentzian widths. These are expressed as a function of wavelength,
are
Gaussian and Lorentzian widths. These are expressed as a function of wavelength,
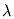 .
.
Figure 2 illustrate the fitting process with the four-component fitting:
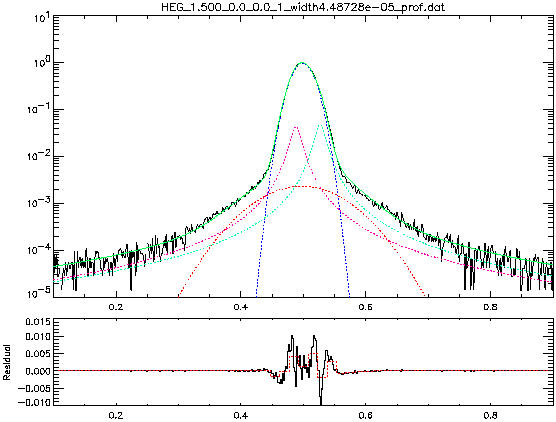
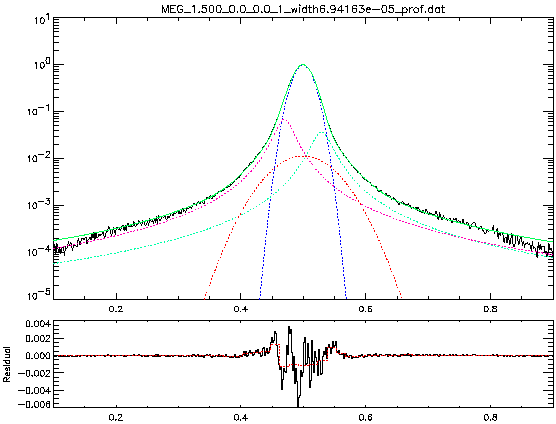
Generally the four-component fitting suffices to describe both its core and wing part of LSFs. However sometimes even the four-component fitting is not sufficient, especially for the MEG line profile at a lower E value. Figure 3 gives this worst example:
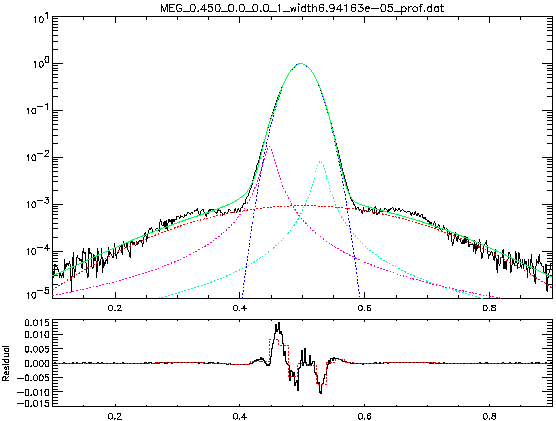
The users should be aware that the LSF library may include such imperfection.
This fitting process was repeated roughly at 20+ different energies per extraction width. Figure 4 shows primary Gaussian widths as a function of energy at the extraction width ~ 9.2'' (~+/- 0.00129 degrees):
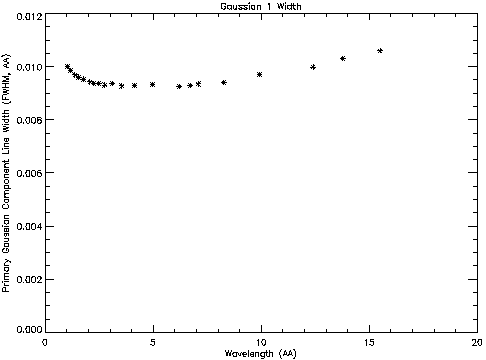
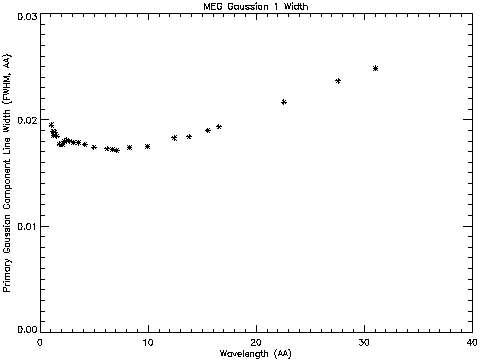
The fitting parameters for amplitude, line position, and width for both two Gaussian and two Lorentzian functions -- i.e., a total of 12 parameters -- are measured and recorded to build the LSF library.
Encircled Energy Fraction (EEFRACS)
We define the term "encircled energy fraction" (EEFRACS) as the ratio of the sum of counts included in the extraction region to the total counts detected on the detector per mono-energetic beam per order. We can evaluate this numerically in MARX simulations. Figure 5 shows the EEFRACS as a function of wavelength for both HEG and MEG:
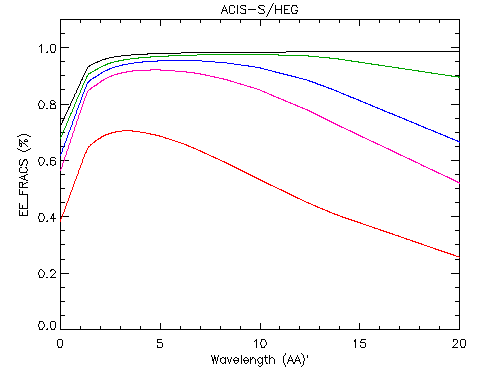
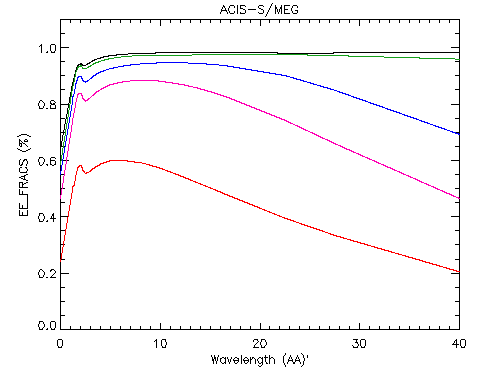
Final Step
All the fitting parameters plus EEFRACS values are tabulated first, and then interpolated with uniform grid points. Then the array of data values are written into a FITS file that meets the requirement of Chandra CALDB. This concludes the building process of the LSF library. [Note that all the tools for making the LSF library can be made available to the public, if they wish to duplicate the effort. However, technical support for such is not provided (but moral support may be).]
The next section describes caveats associated with the use of the LSF library.
| Previous: Generation of LSF Reference Data | Next: Caveats on Using LSF |