Next: 14. wavdetect Parameters & Up: The Detect Reference Manual Previous: 12. Advanced wavdetect: Using Contents
This chapter is a draft copy of the paper "A Wavelet-Based Algorithm for the Spatial Analysis of Poisson Data'' by P.E. Freeman, V. Kashyap, R. Rosner, D.Q. Lamb, Ap. J. Suppl. Series, Vol. 138, p. 185, 2002. The published paper is available online via astro-ph: http://arXiv.org/abs/astro-ph/0108429 .
A wavelet is a member of a family of oscillatory scaleable functions
which deviates from zero within a limited spatial regime, and has zero
normalization. Perhaps the simplest example of such a function is a
positively valued "top hat," with amplitude ![]() and width
and width ![]() ,
flanked by two negatively valued troughs with total integrated area
,
flanked by two negatively valued troughs with total integrated area
![]() . (This in fact describes the Haar wavelet family.) Any function
with zero normalization satisfying the property
. (This in fact describes the Haar wavelet family.) Any function
with zero normalization satisfying the property
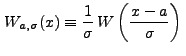 |
(13.1) |
The importance of wavelet functions only began to be recognized in early 1980s, when they were used in the analysis of seismic data (Goupillaud et al. 1984). Wavelets are now used as tools in atomic physics, the study of fractal structures, time series, sound, and image analysis, etc. Slezak, Bijaoui, & Mars (1990) were the first to apply wavelets in astronomy, applying them to galaxy catalogue data to search for statistically significant clusters and voids. The interested reader may find more information on wavelets in Daubechies (1992) or Holschneider (1995).
Wavelet transforms, convolutions of an arbitrary analyzable function with a set of suitably scaled wavelet functions, provides a superior means to detect and characterize sources in an image, compared with classical "sliding-box''13.1 and Fourier methods. Because a wavelet is a function with limited spatial extent, it can be used to determine source locations, like the sliding-box. Unlike the sliding-box, however, it can also be used to identify the dominant frequencies in the analyzed function, i.e. to characterize source shape and extent. Such characterization could also be done with Fourier analysis, but unlike Fourier methods, wavelets determine localized frequency information, as a consequence of their localization in both the spatial and Fourier domains.
The program wtransform applies wavelets to the problem of detecting sources in X-ray data, and the associated program wrecon analyzes the detected sources and constructs the source list. While others have developed codes with similar analysis goals (e.g. Vikhlinin, Forman, & Jones 1994; Rosati et al. 1995; Grebenev, Forman, & Jones 1995), wtransform and wrecon are considerably more complex, e.g. correcting for exposure variation across the field of view (FOV), and making error estimates, while not requiring that the point spread function (PSF) have a particular functional form (which is particularly important for analysis of Chandra images). Another program of similar complexity but using different methods is the palermo wdetect program of Damiani et al. (1997).
In §13.2 we describe the basic recipe one would follow to detect sources in data, without reference to any particular wavelet function. We do this is to underscore the fact that the basic details of the method are not dependent on the choice of wavelet function, so long as that function is simple, with one centralized positive amplitude mode. The fact that the PSF of X-ray detectors often has Gaussian-like shape motivates our use of the Marr wavelet, or "Mexican Hat" (MH) function, which we describe in Appendix 13.5.
The program wtransform uses the correlation of the MH function with
a given image ![]() to identify putative source pixels. In
§13.3 we describe in detail the steps that
wtransform follows, in particular discussing how the program
estimates the local background at each pixel, how it corrects for the
systematic shift that a pixel's correlation value will take if the
exposure varies within the limited spatial extent of the wavelet
function, and how it performs error analysis. In appendices which
relate to §13.3, we present derivations of
analytic quantities related to the MH function (Appendix
13.6), as well as describe the simulations used to
estimate the threshold correlation value for source detection in each
pixel (Appendix 13.7). In
§13.4 we discuss in detail how the source
list is constructed by wrecon , and in an appendix we describe how
wrecon computes a default background image for use in determining
source properties (Appendix 13.8).
to identify putative source pixels. In
§13.3 we describe in detail the steps that
wtransform follows, in particular discussing how the program
estimates the local background at each pixel, how it corrects for the
systematic shift that a pixel's correlation value will take if the
exposure varies within the limited spatial extent of the wavelet
function, and how it performs error analysis. In appendices which
relate to §13.3, we present derivations of
analytic quantities related to the MH function (Appendix
13.6), as well as describe the simulations used to
estimate the threshold correlation value for source detection in each
pixel (Appendix 13.7). In
§13.4 we discuss in detail how the source
list is constructed by wrecon , and in an appendix we describe how
wrecon computes a default background image for use in determining
source properties (Appendix 13.8).
The algorithm by which one uses a simple unimodal wavelet function
![]() to detect sources in a two-dimensional
image
to detect sources in a two-dimensional
image ![]() is conceptually simple.13.2 This function is
convolved with
is conceptually simple.13.2 This function is
convolved with ![]() to produce a "correlation image"
to produce a "correlation image" ![]() :
:
A clump of counts will manifest itself as a local maximum in a
correlation image if the scale sizes
![]() are
approximately the same as, or larger than, the size of the clump. One
can see why this is so more easily if we write
are
approximately the same as, or larger than, the size of the clump. One
can see why this is so more easily if we write
![]() , where
, where ![]() and
and ![]() denote the positive and negative
amplitude portions of the wavelet function, respectively. If the
clump is contained completely within
denote the positive and negative
amplitude portions of the wavelet function, respectively. If the
clump is contained completely within ![]() , then the contribution of
the positive term to
, then the contribution of
the positive term to ![]() outweighs that of the negative term,
producing a maximum.13.3 If the scale sizes are smaller, then
the wavelet function will extend over a smaller region within the
clump, within which the inferred counts amplitude will tend more and
more to a constant. Hence
outweighs that of the negative term,
producing a maximum.13.3 If the scale sizes are smaller, then
the wavelet function will extend over a smaller region within the
clump, within which the inferred counts amplitude will tend more and
more to a constant. Hence
![]() . For larger scale sizes,
the correlation value tends asymptotically to a maximum,
. For larger scale sizes,
the correlation value tends asymptotically to a maximum,
![]() .
.
Source detection boils down to the question: how large must the value
![]() become before we may safely accept that a
source has contributed counts to the observed clump? To answer this,
we compute the Type I error, or the probability that we would
erroneously accept a source when the null hypothesis, that there is no
source, is correct. We compute this quantity, also called the
significance, in each image pixel
become before we may safely accept that a
source has contributed counts to the observed clump? To answer this,
we compute the Type I error, or the probability that we would
erroneously accept a source when the null hypothesis, that there is no
source, is correct. We compute this quantity, also called the
significance, in each image pixel ![]() :
:
If ![]() is estimated from the raw data themselves, this
estimate will be biased if source counts are present, so that
is estimated from the raw data themselves, this
estimate will be biased if source counts are present, so that
![]() . Thus an iterative procedure is used to
remove source counts from the image:
. Thus an iterative procedure is used to
remove source counts from the image:
After this algorithm is used to determine lists of source pixels for many wavelet scale sizes, cross-identification of pixels across scales is performed to create the final source list. This cross-identification allows the weeding out of spurious sources which may be detected even if a high significance threshold is used.
In §13.2, we noted how the condition
![]() 0 can be interpreted to mean that the
0 can be interpreted to mean that the ![]() performs
a "background subtraction." It is thus natural to use a function of
performs
a "background subtraction." It is thus natural to use a function of
![]() to estimate
to estimate ![]() in pixel
in pixel ![]() , if it is a
priori unknown:
, if it is a
priori unknown:
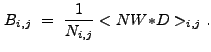 |
(13.4) |
We stress that one should not interpret ![]() blindly as the
actual background amplitude
blindly as the
actual background amplitude
![]() ; it should only be
viewed as a computation made in order to select source pixels. For
instance, if a small wavelet scale is applied in a region with a large
PSF, then
; it should only be
viewed as a computation made in order to select source pixels. For
instance, if a small wavelet scale is applied in a region with a large
PSF, then
![]() around any source, because
the estimate of
around any source, because
the estimate of ![]() is unavoidably biased by the source counts
which lie in the region spanned by
is unavoidably biased by the source counts
which lie in the region spanned by ![]() . In wrecon , we provide a
default method of combining information across scales to estimate
. In wrecon , we provide a
default method of combining information across scales to estimate
![]() (which we discuss in Appendix
13.8); it is this quantity which is used to
help determine source properties.
(which we discuss in Appendix
13.8); it is this quantity which is used to
help determine source properties.
| (13.8) |
Variations in exposure within the limited spatial extent of the MH
function, e.g. caused by the shadows of mirror supports and
ribs, or by the edge of the FOV itself, will reduce the accuracy of
the estimate of ![]() . This quantity may be overestimated or
underestimated, depending upon the location of pixel
. This quantity may be overestimated or
underestimated, depending upon the location of pixel ![]() relative
to regions of reduced exposure, but an overestimate is more damaging,
as it can lead to the detection of a spurious source. An overestimate
will occur if the exposure reduction primarily occurs within
relative
to regions of reduced exposure, but an overestimate is more damaging,
as it can lead to the detection of a spurious source. An overestimate
will occur if the exposure reduction primarily occurs within ![]() . To
see this, let us assume the counts in regions without exposure
variation to be a constant, and that the exposure reduction causes a
reduction in counts
. To
see this, let us assume the counts in regions without exposure
variation to be a constant, and that the exposure reduction causes a
reduction in counts ![]() . Then:
. Then:
| (13.9) |
| (13.10) |
The source counts, ![]() , may also be altered by variations in exposure
if the source is extended; however, correcting
, may also be altered by variations in exposure
if the source is extended; however, correcting ![]() requires knowledge
of
requires knowledge
of
![]() , which is a priori unknown. Also, our prime
motivation for correcting
, which is a priori unknown. Also, our prime
motivation for correcting ![]() is to reduce the number of
spurious sources, and correcting
is to reduce the number of
spurious sources, and correcting ![]() does not help us in this regard.
does not help us in this regard.
In §13.2, we show how the significance is
computed in each pixel. However, for reasons discussed fully in
Appendix 13.7, wtransform does not compute
significances directly, but rather compares each correlation value
![]() with a threshold correlation value
with a threshold correlation value ![]() . This
threshold is found by estimating the lower bound on the integral in
Eq. (13.3), given
. This
threshold is found by estimating the lower bound on the integral in
Eq. (13.3), given ![]() , a user-specified significance
threshold (e.g. 10
, a user-specified significance
threshold (e.g. 10![]() ), and
), and
![]() . If
. If
![]() , pixel
, pixel
![]() is identified as a possible source pixel.
is identified as a possible source pixel.
In wtransform , the user actually specifies two threshold significance
values: ![]() , for source cleansing, and
, for source cleansing, and ![]() . During
iterations,
. During
iterations, ![]() is compared to
is compared to ![]() , which may be set to
be much larger than
, which may be set to
be much larger than ![]() (e.g. 10
(e.g. 10![]() ) to help reduce the
bias caused by source counts in estimates of
) to help reduce the
bias caused by source counts in estimates of ![]() .
.
The analytic calculations of ![]() and
and ![]() involve the
pixel-by-pixel summation of the independent Poisson-distributed random
variable
involve the
pixel-by-pixel summation of the independent Poisson-distributed random
variable ![]() . To compute the variances of these quantities, we
use the general formula
. To compute the variances of these quantities, we
use the general formula
![$\displaystyle V[Y]~=~V[\sum_m a_m X_m]~=~\sum_m a_m^2 V[X_m] + 2 \sum_m \sum_{n > m} a_m a_n {\rm cov}[X_m,X_n] .$](img242.gif) |
(13.13) |
![$ V[Y]~\approx~\sum_m \left(\frac{{\partial}Y}{{\partial}X_m}\right)^2
V[X_m]$](img247.gif) .
.
![$\displaystyle ~\sum_{i'} \sum_{j'} \left[W_{i-i',j-j'}-\left(\sum_{i''} \sum_{j...
...,j'-j''}(E_{i,j}-E_{i'',j''})}{<NW{\ast}E>_{i'',j''}} \right) \right] D_{i',j'}$](img261.gif) |
|||
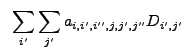 |
![$\displaystyle V[C_{{\rm cor},i,j}]~=~\sum_{i'} \sum_{j'} a_{i,i',i'',j,j',j''}^2 D_{i',j'}$](img263.gif) |
(13.19) |
| (13.20) |
The program wrecon is used to construct the final source list after wtransform has been run at all desired scales. To construct this list, it uses:
The flux image is created by smoothing the raw data, then subtracting the normalized background from the smoothed image13.5 on a pixel-by-pixel basis:
The scale pairs
![]() at which to compute the flux
images are user-specified; the number of pairs can be less than the
number of wavelet scale pairs examined overall. Using fewer pairs
reduces computation time, but may lead to a less-precise determination
of source properties. Hereafter, we assume that
at which to compute the flux
images are user-specified; the number of pairs can be less than the
number of wavelet scale pairs examined overall. Using fewer pairs
reduces computation time, but may lead to a less-precise determination
of source properties. Hereafter, we assume that
![]() , forcing symmetric wavelets.
, forcing symmetric wavelets.
To determine source properties, it is necessary to define a "cell" on
the detector, in which some portion of a source's counts are
detected. If we choose the size and shape of the cell, then we need
detailed knowledge of the PSF to estimate the fraction of a source's
counts that are recorded in the cell. However, wrecon and the other
Chandra detection algorithms assume no details about a detector's PSF
except for its characteristic size
![]() , which is computed
for Chandra data using the routine psf_calc_size; its
functional form is unknown. But even if we did have detailed knowledge
of the PSF, its use would provide a good estimate of the total source
counts only if the source were point-like.
, which is computed
for Chandra data using the routine psf_calc_size; its
functional form is unknown. But even if we did have detailed knowledge
of the PSF, its use would provide a good estimate of the total source
counts only if the source were point-like.
wrecon uses the flux images to define the source cell. In regions
where there are no sources, the mean value of ![]() is zero; only in the
vicinity of sources does
is zero; only in the
vicinity of sources does ![]() deviate markedly from zero. Hence
wrecon defines the source cell by
deviate markedly from zero. Hence
wrecon defines the source cell by
A cell defined in this manner has advantageous properties:
This approach is not always optimal when analyzing extended sources:
such sources may have more than one local maximum in counts space,
leading to multiple "sources" being listed. One way to counteract
this is to set
![]() , as this will
increase the probability of the extended object being associated with
one maximum in
, as this will
increase the probability of the extended object being associated with
one maximum in ![]() -space (which will ensure a sufficiently large
cell). However, it also increases the probability that point sources
in the vicinity of the extended source will be "swallowed up" by the
larger source cell, so care must be exercised when interpreting
derived source properties such as count rate. This approach is also
not optimal if PSF is bimodal, as it is far off-axis for Chandra ; in
this case, wtransform will output two correlation maxima for a
well-sampled source, and wrecon will characterize each maximum
independently of the other. Only with the a posteriori
application of a detailed PSF can the two "sources" be properly
combined.
-space (which will ensure a sufficiently large
cell). However, it also increases the probability that point sources
in the vicinity of the extended source will be "swallowed up" by the
larger source cell, so care must be exercised when interpreting
derived source properties such as count rate. This approach is also
not optimal if PSF is bimodal, as it is far off-axis for Chandra ; in
this case, wtransform will output two correlation maxima for a
well-sampled source, and wrecon will characterize each maximum
independently of the other. Only with the a posteriori
application of a detailed PSF can the two "sources" be properly
combined.
It is also possible for a source cell to contain two or more underlying sources. This is indicated when there are multiple correlation maxima in the source cell at the PSF scale. The code indicates such a condition with a flag in the source list; it does not currently attempt to "break up" the cell to refine source property estimates.
To create the source list, wrecon examines the lists of correlation
maxima in ascending order of wavelet size. If the location of a
maximum ![]() is not already associated with a source cell (see
below), it will be provisionally associated with a real source if
is not already associated with a source cell (see
below), it will be provisionally associated with a real source if
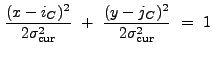 |
After determining for the putative source its cell and properties,
wrecon first scans through the lists of all correlation maxima at
all scales, and marks as "examined" those which lie within the
current source cell, and then verifies that the putative source
appears at one or more scales
![]() . It does this by
determining the scale size closest to the PSF size,
. It does this by
determining the scale size closest to the PSF size,
![]() (by minimizing
(by minimizing
![]() ),
then counting the number of correlation maxima that lie within the
source cell for
),
then counting the number of correlation maxima that lie within the
source cell for
![]() . If the number is
zero, wrecon rejects the putative source.
. If the number is
zero, wrecon rejects the putative source.
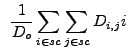 |
(13.22) | ||
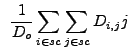 |
(13.23) |
A preferred weighting function would be the source flux
![]() , but its use greatly complicates
the computation of variances
, but its use greatly complicates
the computation of variances
![]() and
and
![]() . (For similar reasons,
. (For similar reasons, ![]() is not used as a weighting
function.)
is not used as a weighting
function.) ![]() and
and
![]() will give
similar estimates if the source is strong or if background is small.
will give
similar estimates if the source is strong or if background is small.
The variance of the location estimate,
![]() , is
estimated using Eq. (13.14):
, is
estimated using Eq. (13.14):
![$\displaystyle ~\sum_{i \in sc}\sum_{j \in sc} \left(\frac{{\partial}x_{\rm source}}{{\partial}D_{i,j}}\right)^2 V[D_{i,j}]$](img298.gif) |
|||
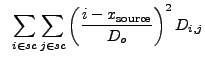 |
(13.24) |
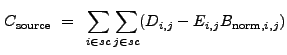 |
(13.25) |
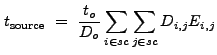 |
(13.27) |
![]() is computed in an analogous manner to
is computed in an analogous manner to
![]() , by replacing
, by replacing ![]() with
with
![]() :
:
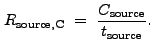 |
(13.29) |
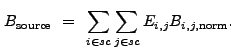 |
(13.31) |
![$\displaystyle V[B_{\rm source}]~\approx~\sum_{i \in sc}\sum_{j \in sc} E_{i,j}^2B_{i,j,{\rm norm}} .$](img321.gif) |
(13.32) |
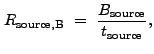 |
(13.33) |
![$\displaystyle V[R_{\rm source,B}]~\approx~\frac{1}{t_{\rm source}^2} \left( V[B_{\rm source}] + R_{\rm source,B}^2V[t_{\rm source}] \right) .$](img323.gif) |
(13.34) |
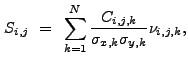 |
(13.35) |
The source detection algorithm we present in this paper should not depend on the details of function itself, at least for simple wavelets which have one central positive mode. In this Appendix, we describe the Marr wavelet function, or "Mexican Hat function,'' (MH) which is used by wtransform and wrecon .
A wavelet function may be derived from a real-valued, non-negative,
infinitely differentiable function ![]() that satisfies the
condition
that satisfies the
condition
![]() 1 (see, e.g., Holschneider
1995). One function that satisfies these requirements is the Gaussian:
1 (see, e.g., Holschneider
1995). One function that satisfies these requirements is the Gaussian:
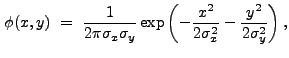 |
(13.36) |
The MH has a positive kernel surrounded by a negative annulus; the
boundary between these two regions is an ellipse with axis-lengths
![]() and
and
![]() :
:
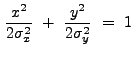 |
(13.38) |
The MH function has several advantageous properties which motivate its use.
If the width of the wavelet function is of order the size of the image
pixel, then using FFTs to compute
![]() and other related
quantities becomes impractible. To determine
and other related
quantities becomes impractible. To determine ![]() , for instance,
we integrate
, for instance,
we integrate ![]() on a pixel-by-pixel basis, as shown in
Eq. (13.7).
on a pixel-by-pixel basis, as shown in
Eq. (13.7).
We substitute the form of ![]() in Eq. (13.37) into
Eq. (13.7):
in Eq. (13.37) into
Eq. (13.7):
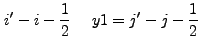 |
|||
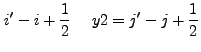 |
If we expand Eq. (13.39), we find that there are two basic
integrals which must be performed. The first is:
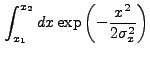 |
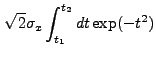 |
||
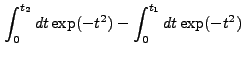 |
|||
![$\displaystyle \sqrt{\frac{\pi}{2}} \sigma_x \left[{\rm erf}\left(\frac{x_2}{\sqrt{2}\sigma_x}\right) - {\rm erf}\left(\frac{x_1}{\sqrt{2}\sigma_x}\right)\right]$](img352.gif) |
|||
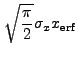 |
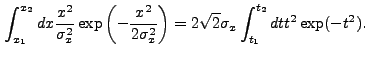 |
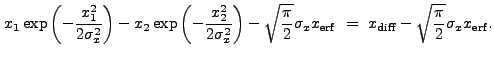 |
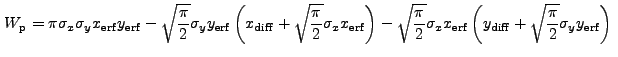 |
(13.40) |
If exposure variations and the FOV edge may be ignored in the
computation of the background, then we may replace
![]() in Eq. (13.5) with a background normalization factor, which
we derive here.
in Eq. (13.5) with a background normalization factor, which
we derive here.
The overall normalization of the MH function is zero. Hence the background normalization factor may be derived by integrating over its positive core:
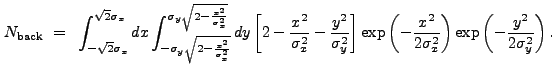 |
(13.41) |
We evaluate the second integral using integration by parts:
![$\displaystyle ~2{\pi}\frac{\sigma_{y}}{\sigma_{x}} \left[r^2\exp\left(-\frac{r^2}{2\sigma_{x}}\right)\mid_0^{\sqrt{2}\sigma_{x}}\right]$](img375.gif) |
|||
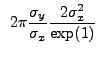 |
|||
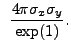 |
(13.46) |
The Fourier Transform of ![]() is
is
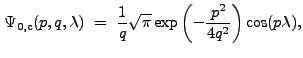 |
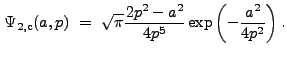 |
To compute the error of the correlation values in each pixel, we
calculate
![]() using an analytic Fourier Transform
using an analytic Fourier Transform
![]() . The derivation of this function is similar to the
derivation of
. The derivation of this function is similar to the
derivation of ![]() . A new integral which appears is:
. A new integral which appears is:
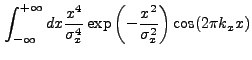 |
(13.52) |
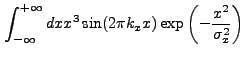 |
(13.53) |
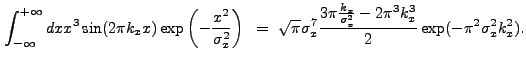 |
(13.54) |
The final solution is
| (13.55) |
An image pixel ![]() is associated with an astronomical source if
the significance
is associated with an astronomical source if
the significance ![]() of its correlation value
of its correlation value ![]() is
greater than a user-defined threshold significance
is
greater than a user-defined threshold significance ![]() :
:
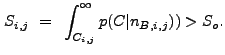 |
We find that
![]() does not have analytic form for
those values of
does not have analytic form for
those values of ![]() most likely to be seen in analyses of Chandra images, so we must estimate this distribution using simulations. The
computation time needed for such simulations means that we cannot
accurately assign significances to pixels if
most likely to be seen in analyses of Chandra images, so we must estimate this distribution using simulations. The
computation time needed for such simulations means that we cannot
accurately assign significances to pixels if
![]() . So
instead of computing the significance, wtransform compares the value
of
. So
instead of computing the significance, wtransform compares the value
of ![]() in each pixel with a threshold correlation value
in each pixel with a threshold correlation value
![]() , defined by the equation
, defined by the equation
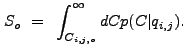 |
(13.56) |
By analyzing over 50,000 simulated images, we are able to determine 25
values of ![]() in each
in each
![]() bin, for values of
bin, for values of ![]() 10
10![]() , using the central 68% (17) of the values to estimate
variances. We fit simple functions to the estimated threshold values,
using the
, using the central 68% (17) of the values to estimate
variances. We fit simple functions to the estimated threshold values,
using the ![]() method and the estimated variances. We present our
results below. These functions describe the observed threshold values
well, except in the regime
method and the estimated variances. We present our
results below. These functions describe the observed threshold values
well, except in the regime
![]() and
and
![]() , where a binned look-up table is used instead. We note that these
fits allow us in principle to compute threshold correlation values for
significance values below our computational lower limit
, where a binned look-up table is used instead. We note that these
fits allow us in principle to compute threshold correlation values for
significance values below our computational lower limit ![]() 10
10![]() (such as for
(such as for ![]() 10
10![]() , the significance
corresponding to one false source pixel in an Chandra HRC image).
, the significance
corresponding to one false source pixel in an Chandra HRC image).
In the regime
![]() and
and
![]() ,
,
![]() is well-described by the parabola:
is well-described by the parabola:
| (13.57) |
In the regime
![]() ,
,
![]() is described by
the function
is described by
the function
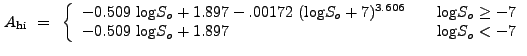
For values
![]() , we find that we must sometimes use
the linear equation
, we find that we must sometimes use
the linear equation
| (13.59) |
| (13.60) |
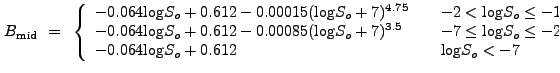
If the probability sampling distribution is Gaussian with width
![]() , then the significance is given by:
, then the significance is given by:
If the user does not provide a normalized background image, wrecon will create such an image by combining the normalized background
images that wtransform creates at each wavelet scale:
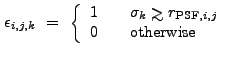
and ![]() is the number of scales used. "
is the number of scales used. "
![]() "
denotes all
"
denotes all
![]() , along with the largest
, along with the largest
![]() . For instance, if
. For instance, if
![]() = 9 pixels,
= 9 pixels,
![]() 1 for the standard progression values
1 for the standard progression values ![]() =
[8,8
=
[8,8![]() ,16,...], and
,16,...], and
![]() 0 for
0 for ![]() =
[...4,4
=
[...4,4![]() ]. We exclude the smallest scales because for
]. We exclude the smallest scales because for
![]() , the background is greatly overestimated in the
vicinity of sources. The weighting reflects that the area of the FOV
used to estimate the background goes as
, the background is greatly overestimated in the
vicinity of sources. The weighting reflects that the area of the FOV
used to estimate the background goes as ![]() . The default
background for wrecon is then:
. The default
background for wrecon is then:
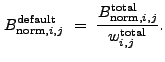 |
(13.64) |
We may algebraically manipulate the combination of
eqs. (13.5), (13.62), and (13.63), to
express the default normalized background as
Damiani, F., Maggio, A., Micela, G., & Sciortino, S. 1997, ApJ 483, 350
Daubechies, I. 1992, Ten Lectures on Wavelets (Philadelphia: SIAM)
Eadie, W. T., Drijard, D., James, F. E., Roos, M., & Sadoulet, B. 1971, Statistical Methods in Experimental Physics (Amsterdam: North-Holland)
Goupillaud, P., Grossmann, A., & Morlet, J. 1984, Geoexploration 23, 85
Gradshteyn, I., & Ryzhik, I. 1980, Table of Integrals, Series, and Products (San Diego: Academic Press)
Grebenev, S. A., Forman, W., & Jones, C. 1995, ApJ 445, 607
Holschneider, M. 1995, Wavelets: An Analysis Tool (Oxford: Oxford University Press)
Micela, G., Sciortino, S., Kashyap, V., Harnden, F. R., Jr., & Rosner, R. 1996, ApJS 102, 75
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P.1992, Numerical Recipes (Cambridge: Cambridge Univ. Press)
Rosati, P., Della Cecai, R., Burg, R., Norman, C., & Giacconi, R. 1995, ApJL 445, 11
Slezak, E., Bijaoui, A., & Mars, G. 1990, A&A 227, 301
Vikhlinin, A., Forman, W., & Jones, C. 1994, ApJ 435, 162
cxchelp@head.cfa.harvard.edu