Sherpa Optimization Methods
-
Available Optimization Methods: each optimization method described in detail.
Introduction
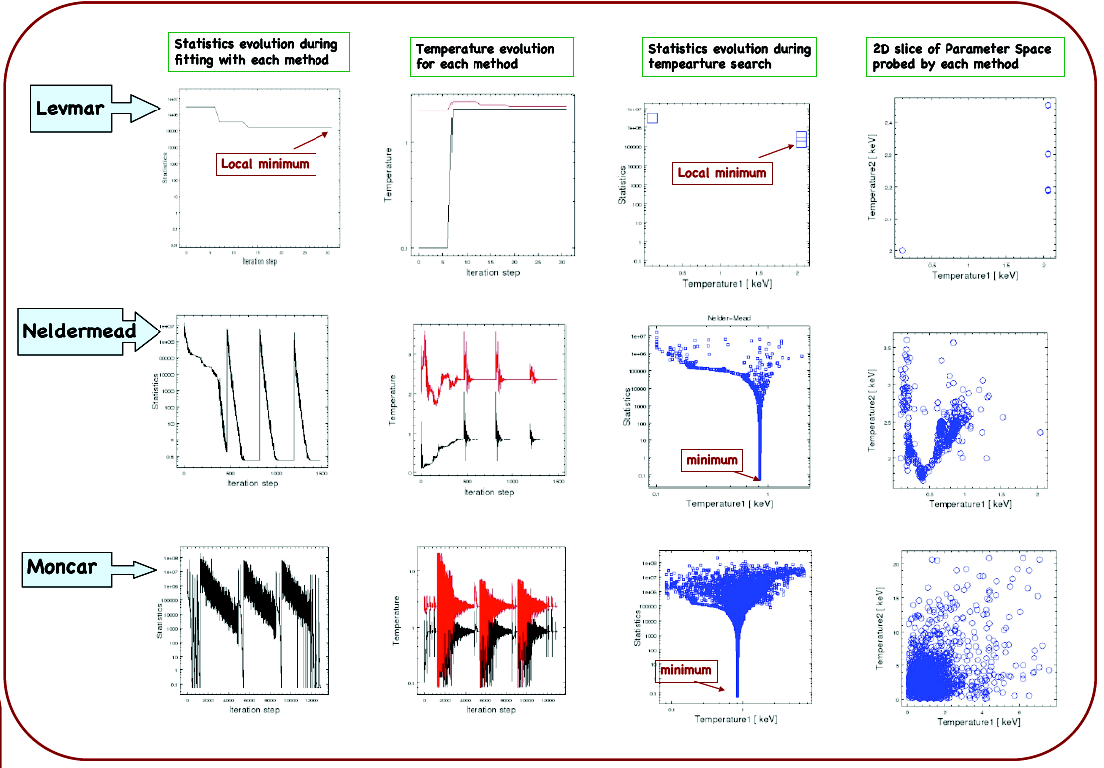
The "forward-fitting" algorithm employed by the Sherpa software package is a standard technique used to model X-ray data. A statistic, usually an assumed weighted chi2 or Poisson likelihood (e.g. Cash), is minimized in the fitting process to obtain a set of the best model parameters. Astronomical models often have complex forms with many parameters that can be correlated (e.g. an absorbed power-law); minimization is not trivial in such a setting, as the statistical parameter space becomes multimodal, and finding the global minimum is difficult. Therefore we have developed several optimization algorithms in Sherpa which target a wide range of minimization problems. Two local minimization methods were built: the Levenberg-Marquardt algorithm was obtained from the MINPACK subroutine LMDIF and modified to achieve the required robustness; and the Nelder-Mead simplex method has been implemented in-house based on variations of the algorithm described in the literature. A global search Monte-Carlo method has been implemented following a differential evolution algorithm presented by Storn and Price (1997). Below we present the methods in Sherpa and discuss their performance in complex X-ray spectral model application to Chandra high S/N data.
Details
Optimization Methods
- Optimization - finding a parameter value for which a statistics function has a minimum (or a maximum).
-
Requirements for the optimization methods in Sherpa:
- Applicable to a variety of problems in modeling X-ray data, e.g., low- and high-counts Poisson data.
- Robust when applied to complex models.
Local Methods:
- Levenberg-Marquardt
-
- Calculates derivatives of a statistics function over the parameter space of the function .
- Appropriate for chi2 statistics.
- Convergence when the difference in the statistics in the iterative steps is smaller than the required tolerance.
- Fast, but very dependent on initial conditions; known to fail in complex cases with poor initial parameter values.
- Sherpa's levmar method is based on the LMDIF subroutine (from the MINPACK library of FORTRAN subroutines).
- Simplex
-
-
Starts from an initial set of parameters and then
improves the parameters in a continuous fashion:
- Non-derivative method, no gradient information.
- Convergence when the statistics at the vertices are small or the simplex is small.
- Sherpa includes simplex as an implementation of the Nelder-Mead algorithm (Nelder & Mead, 1965, Computer Journal, vol 7, 308-313).
-
Starts from an initial set of parameters and then
improves the parameters in a continuous fashion:
Global Methods:
- Monte-Carlo
-
- Random selection of parameters from the entire permitted parameter space.
- Includes conditions for a "smart" selection of parameters to improve efficiency of the search.
- Sherpa's moncar method is an implementation of the Differential Evolution algorithm based on Storn and Price (J. Global Optimization 11, 341-359, 1997; originally available at http://www.icsi.berkeley.edu/~storn/code.html).
- Gridsearch
-
Evaluates the fit statistic for each point in a user-specified parameter space grid, and returns the parameter values associated with the grid point with the lowest value of the fit statistic (the best match).
Summary
- levmar is fast, very sensitive to initial parameters, and performs well for simple models, e.g. power-law or single-temperature models, but fails to converge with complex models.
- neldermead and moncar are both very robust and converge to the global minimum in complex model cases.
- neldermead is more efficient than moncar, but moncar probes a larger part of the parameter space.
- moncar or neldermead should be used when fitting complex models with correlated parameters.
New in CIAO 4.18 is support for some of the optimizers provided by
the
SciPy
and
optimagic
packages. These can be used if those provided by Sherpa are
insufficient.
![[New]](../imgs/new.gif) (16 Dec 2025)
(16 Dec 2025)
- Standard methods
-
sherpa> list_methods() ['gridsearch', 'levmar', 'moncar', 'neldermead', 'simplex']
- With SciPy installed
-
sherpa> list_methods() ['gridsearch', 'levmar', 'moncar', 'neldermead', 'scipy_basinhopping', 'scipy_differentialevolution', 'scipy_direct', 'scipy_dualannealing', 'scipy_minimize', 'scipy_shgo', 'simplex']
- With optimagic installed
-
Installing optimagic automatically installs SciPy:
sherpa> list_methods() ['gridsearch', 'levmar', 'moncar', 'neldermead', 'optimagic', 'scipy_basinhopping', 'scipy_differentialevolution', 'scipy_direct', 'scipy_dualannealing', 'scipy_minimize', 'scipy_shgo', 'simplex']
Tracking the optimizer
The fit call has two methods that can track the parameter space searched by the optimizer:
-
if the outfile parameter is set then the parameter values, along with the statistic value, will be written to the given file (if `clobber` is set or the file does not exist). This file is an ASCII text file.
sherpa> fit(outfile="fit.txt", clobber=True) sherpa> !head -5 fit.txt # nfev statistic gal.nH pl.gamma pl.ampl 0.000000e+00 5.431454e+10 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 5.431454e+10 1.000000e+00 1.000000e+00 1.000000e+00 2.000000e+00 5.431118e+10 1.000345e+00 1.000000e+00 1.000000e+00 3.000000e+00 5.426009e+10 1.000000e+00 1.000345e+00 1.000000e+00
-
if the record_steps=True is set then the parameter and statistic values will be stored in the record_steps attribute of the FitResults structure.
![[New]](../imgs/new.gif) (16 Dec 2025)
(16 Dec 2025)
sherpa> fit(record_steps=True) sherpa> res = get_fit_results() sherpa> res.record_steps[:5] array([(0, 5.43145420e+10, 1. , 1. , 1. ), (1, 5.43145420e+10, 1. , 1. , 1. ), (2, 5.43111759e+10, 1.00034527, 1. , 1. ), (3, 5.42600895e+10, 1. , 1.00034527, 1. ), (4, 5.43520566e+10, 1. , 1. , 1.00034527)], dtype=[('nfev', '<i8'), ('statistic', '<f8'), ('gal.nH', '<f8'), ('pl.gamma', '<f8'), ('pl.ampl', '<f8')])
Global Methods: Monte-Carlo