Available Optimization Methods
The primary task of Sherpa is to fit a model 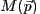 to a
set of observed data, where
to a
set of observed data, where 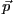 denotes the model parameters. An optimization
method is one that is used to determine the vector of model
parameter values,
denotes the model parameters. An optimization
method is one that is used to determine the vector of model
parameter values, 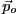 , for which the chosen fit statistic is minimized.
, for which the chosen fit statistic is minimized.
Optimization is complicated because there is no guarantee that, for a given model and dataset, there will not be multiple local fit-statistic minima. Thus Sherpa provides a number of optimization methods, each of which has different advantages and disadvantages. The default optimization method is levmar, which is a robust method for finding the nearest local fit-statistic minimum (but not necessarily the global minimum). The user can change the method using the set_method command.
The relative merits of each of the different optimization methods, and accompanying advice for use in Sherpa, are available here.
The following optimization methods are available in Sherpa:
levmar
The Levenberg-Marquardt optimization method.
The Levenberg-Marquardt method is an interface to the MINPACK subroutine lmdif to find the local minimum of nonlinear least squares functions of several variables by a modification of the Levenberg-Marquardt algorithm (J.J. More, "The Levenberg Marquardt algorithm: implementation and theory," in Lecture Notes in Mathematics 630: Numerical Analysis, G.A. Watson (Ed.), Springer-Verlag: Berlin, 1978, pp.105-116).
See the 'levmar' ahelp file for the available method options.
To set the optimization method to 'levmar' and then confirm the new value:
sherpa> set_method("levmar")
sherpa> get_method_name()
'levmar'
moncar
A Monte Carlo search of parameter space.
The Monte Carlo optimization method is an implementation of the differential evolution algorithm.
Differential Evolution
A population of fixed size which contains n-dimensional vectors of (where n is the number of free parameters) are randomly initialized. At each iteration, a new n-dimensional vector is generated by combining vectors from the pool of population, the resulting trial vector is selected if it lowers the objective function. For more details see:
Storn, R. and Price, K. "Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces." J. Global Optimization 11, 341-359, 1997.
or http://www.icsi.berkeley.edu/~storn/code.html
See the 'montecarlo' ahelp file for the available method options.
To set the optimization method to 'moncar' and then confirm the new value:
sherpa> set_method("moncar")
sherpa> get_method_name()
'moncar'
Nelder-Mead Simplex
Nelder-Mead simplex optimization method.
The Nelder-Mead Simplex algorithm, devised by J.A. Nelder and R. Mead (Computer Journal, 1965, vol 7, pp 308-313), is a direct search method of optimization for finding local minimum of an objective function of several variables. The implementation of Nelder-Mead Simplex algorithm is a variation of the algorithm outlined in the following two papers:
- Jeffrey C. Lagarias, James A. Reeds, Margaret H. Wright, Paul E. Wright "Convergence Properties of the Nelder-Mead Simplex Algorithm in Low Dimensions", SIAM Journal on Optimization,Vol. 9, No. 1 (1998), pages 112-147. http://citeseer.ist.psu.edu/3996.html
- Wright, M. H. (1996) "Direct Search Methods: Once Scorned, Now Respectable" in Numerical Analysis 1995 (Proceedings of the 1995 Dundee Biennial Conference in Numerical Analysis) (D.F. Griffiths and G.A. Watson, eds.), 191-208, Addison Wesley Longman, Harlow, United Kingdom. http://citeseer.ist.psu.edu/155516.html
As noted in the paper, terminating the simplex is not a simple task:
For any non-derivative method, the issue of termination is problematical as well as highly sensitive to problem scaling. Since gradient information is unavailable, it is provably impossible to verify closeness to optimality simply by sampling f at a finite number of points. Most implementations of direct search methods terminate based on two criteria intended to reflect the progress of the algorithm: either the function values at the vertices are close, or the simplex has become very small.
Either form of termination-close function values or a small simplex-can be misleading for badly scaled functions.
See the 'neldermead' ahelp file for the available method options.
To set the optimization method to Nelder-Mead with 'neldermead' or 'simplex', and then confirm the new value:
sherpa> set_method("neldermead")
sherpa> get_method_name()
'neldermead'
sherpa> set_method("simplex")
sherpa> get_method_name()
'neldermead'
Gridsearch
Grid searching optimization method
The Sherpa grid searching optimization method, "gridsearch", is meant to be used with the Sherpa template model. This method evaluates the fit statistic for each point in the parameter space grid provided by the user; the best match is the grid point with the lowest value of the fit statistic. gridsearch reports back the parameter values associated with this point.
In the example below, a collection of template models is loaded into the Sherpa model instance 'tbl', and fit to data set 'source.dat' using the Sherpa grid-searching optimization method. The parameters of the template model which best matches the data are returned.
sherpa> load_ascii('source.dat', ncols=3, dstype=Data1D)
sherpa> load_template_model('tbl', 'table.txt')
sherpa> set_model(tbl)
sherpa> set_method('gridsearch')
sherpa> set_method_opt('sequence', tbl.parvals)
sherpa> fit()
user-defined method
A user-defined method.
It is possible for the user to create and implement his or her own fit optimization method in Sherpa. Currently, there does not exist a high-level function for loading into a Sherpa a user-defined method (analogous to 'load_user_stat' for defining a fit statistic), therefore it must be done by defining the method in a separate script (module) which gets imported into Sherpa (either via a fitting script or directly in an interactive session).
In the example Python script fminpowell.py, the Powell optimization method is defined in the 'ScipyPowell()' class, which gets imported into Sherpa by typing "from fminpowell import ScipyPowell" at the Sherpa prompt (or by adding this line to the top of a script), as shown below:
sherpa> from fminpowell import ScipyPowell sherpa> load_data(1, "data1.dat", 3) sherpa> set_model(polynom1d.m1) sherpa> thaw(m1.c1) sherpa> thaw(m1.c2) sherpa> thaw(m1.c3) sherpa> set_method(ScipyPowell()) sherpa> fit()
In the example above, the optimization method defined by the user is imported into Sherpa from the Python module 'fminpowell', and selected with the Sherpa set_method command as the optimization method to be used for fitting data set 'data1.dat'.
sigma-rejection iterative fitting method
The sigma-rejection iterative fitting method.
Sigma-rejection is an iterative fitting method which calls the chosen fit optimization method (levmar, simplex, or moncar) several times during a fit, instead of just once, until the fit can no longer be improved. The fit statistic and optimization methods are selected independently of the sigma-rejection iterative fitting method. Sigma-rejection is based upon the IRAF method SFIT; in successive fits, data points for which ((data - model) / error) exceeds a specified threshold are added to a filter and automatically excluded from the next fit. Iterations cease when there is no change in the filter from one iteration to the next, or when the fit has iterated a user-specified maximum number of times.
See the set_iter_method_opt or get_iter_method_opt ahelp files for the available method options.
Iterative fitting with sigma-rejection takes effect when the fit function is called, after changing the current iterative fitting method from the default value of 'none' to 'sigmarej', as demonstrated below with the set_iter_method and associated commands:
sherpa> print(get_iter_method_name()) none sherpa> list_iter_mthods() ['none', 'primini', 'sigmarej'] sherpa> set_iter_method("sigmarej") sherpa> print(get_iter_method_opt()) {'lrej': 3, 'maxiters': 5, 'grow': 0, 'name': 'sigmarej', 'hrej': 3} sherpa> set_iter_method_opt("maxiters", 10) sherpa> fit()